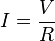Verification of ohm’s law using ammeter and voltmeter
Ohm’s law states that the current through a conductor between two points is directly proportional to the potential difference across the two points. Introducing the constant of proportionality, the resistance,[1] one arrives at the usual mathematical equation that describes this relationship:
where I is the current through the conductor in units of amperes, V is the potential difference measured across the conductor in units of volts, and R is the resistance of the conductor in units of ohms. More specifically, Ohm’s law states that the R in this relation is constant, independent of the current.
The law was named after the German physicist Georg Ohm, who, in a treatise published in 1827, described measurements of applied voltage and current through simple electrical circuits containing various lengths of wire. He presented a slightly more complex equation than the one above (see History section below) to explain his experimental results. The above equation is the modern form of Ohm’s law.
In physics, the term Ohm’s law is also used to refer to various generalizations of the law originally formulated by Ohm. The simplest example of this is:
where J is the current density at a given location in a resistive material, E is the electric field at that location, and σ is a material dependent parameter called the conductivity. This reformulation of Ohm’s law is due to Gustav Kirchhoff.
Verification of ohm’s law using ammeter and voltmeter
Click here to see the Video Clip of this Experiment
Verification of ohm’s law using ammeter and voltmeter
To Download Verification of ohm’s law using ammeter and voltmeter Click Here
Verification of ohm’s law using ammeter and voltmeter
Verification of ohm’s law using ammeter and voltmeter
Verification of ohm’s law using ammeter and voltmeter
Verification of ohm’s law using ammeter and voltmeter
