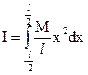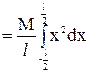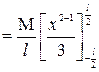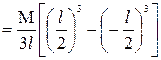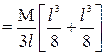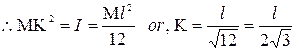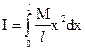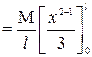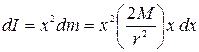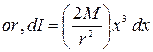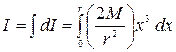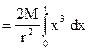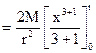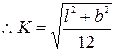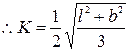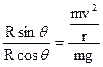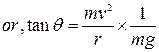Laws Of Rotational Motion (Part-2)
Contents
Laws Of Rotational Motion (Part-2)
Laws Of Rotational Motion (Part-2)
Perpendicular axis theorem:
The moment of inertia of a plane lamina about an axis perpendicular to the plane is equal to the sum of the moments of inertia about two mutually perpendicular axis in the plane of the lamina such that the three mutually perpendicular axes have a common point of intersection.
Explanation: If Ix and Iy be the moments of inertia of a plane
lamina about perpendicular axes, OX and OY, which lie on the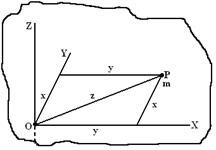
plane of the lamina and intersect each other at O, (Figure Right
hand side) the moment of inertia Iz about an axis, say OZ,
passing through O and perpendicular to the plane of the lamina,
is given by, Ix + Iy = Iz
Proof: Let us consider a plane lamina having axes OX and OY in the plane of the lamina. The axis OZ passes through O and perpendicular to the plane of the lamina. Let the lamina is composed of large number of particles of mass m. Let a particle of m be at P with co-ordinates (x,y) and located at a distance r from O. Here O is the intersection of the three axes.
Now the moment of inertia of the particle P about the axis
OZ = mr2 = m(x2+y2) [∵ r2 = x2+y2]
The moment of inertia of the whole lamina about the axis OX is given by,
Ix= Σ my2
Similarly, the moment of inertia of the whole lamina about the axis OY is given by,
Iy= Σ mx2
The moment of inertia of the whole lamina about OZ axis,
Iz= Σ mr2= Σm(x2+y2)
=Σmx2+Σmy2
= Ix + Iy
Iz = Ix+Iy So, the theorem is Proved.
Laws Of Rotational Motion (Part-2)
Parallel axis theorem:
The moment of inertia of a body about any axis is equal to the sum of the moment of inertia of the body about a parallel axis passing through the center of mass and the product of the mass of the body and the square of perpendicular distance between the two parallel axes.
Explanation: Let AB an axis on the plane of the paper and CD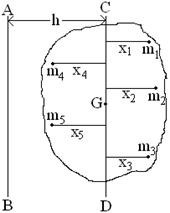
Is another axis parallel to AB. Let the axis CD pass through center of
mass G of the plane lamina (Fig: Right hand side). The distance between
AB and CD axis is h. Now if the moment of inertia of the lamina with
respect to AB and CD axis are respectively I and IG, then according to
this theorem
I=IG+Mh2
Proof: Let the lamina be composed of particles of mass m1, m2, m3 etc. and the respective distance from the axis CD are x1, x2, x3, etc. Then moment of inertia of the particle of mass m1 about axis AB =m1(x1+h)2 = m1x12+m1h2+2m1x1h
Similarly, moment of inertia of the particle of mass m2 about axis AB
= m2x22+m2h2+2m2x2h
And for m3 =m3x32+m3h2+2m3x3h
Now if I is the moment of inertia of the whole lamina about AB, then I will be the summation of the moment of inertia of individual particles i.e.
∴ I = m1x12+m1h2+2m1x1h + m2x22+m2h2+2m2x2h + m3x32+m3h2+2m3x3h + … … …
= Σ mx2+h2Σm+2hΣmx
Here, Σmx= total moment of the mass of the whole lamina about axis CD. But the weight of the lamina is acting downward along the line CD through the point G. So moment of the mass of the lamina about CD is zero.
i.e., Σmx = 0
Again, Σm = M and Σ mx2=IG
∴ I =IG+Mh2+0 = IG+Mh2
Hence the theorem is proved.
Laws Of Rotational Motion (Part-2)
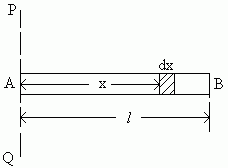
Determination of Moment of inertia and radius of gyration of a thin uniform rod about an axis through its center and perpendicular to its length:
Let AB be a thin uniform rod of length land mass M, free to rotate about the axis CD which is passing through the center and perpendicular to the length of the rod (In the figure below) The moment of inertia about the axis CD is to be found out.
Since the rod is uniform, the mass per unit length ![]()
So at distance x from the axis CD, let dx be a small length whose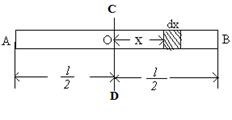
mass, ![]() As dxis very small, we can consider all
As dxis very small, we can consider all
the particles in dx are at same distance from CD. So moment of inertia of dx about axis CD ![]()
Now integrating the above equation within limits x = – l/2 to x = l/2 we get moment of inertia of the entire rod.
Let K be the radius of gyration,
Determination of Moment of inertia and radius of gyration of a thin uniform rod about an axis through one end of the rod perpendicular to its length:
Let AB be a thin uniform rod of length land mass M, free to rotate about the axis CD which is passing through one end of the rod and perpendicular to the length AB of the rod (In the figure below) The moment of inertia about the axis CD is to be found out.
Since the rod is uniform, the mass per unit length ![]()
So at distance x from the axis CD, let dxbe a small length whose
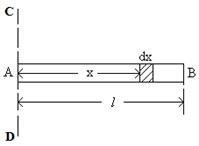 mass,
mass, ![]() As dx is very small, we can consider all
As dx is very small, we can consider all
the particles in dx are at same distance from CD. So moment
of inertia of dx about axis CD ![]()
Now integrating the above equation within limits x = 0 to x = l we get moment of inertia of the entire rod.
Let K be the radius of gyration,
Determination of Moment of inertia and radius of gyration of a circular disk about an axis perpendicular to its plane passing through the center:
Let ABC be a circular disc and let r and Mare respectively its radius and mass. Let O be the center of the disc and PQ its axis about which the disc rotates. The moment of inertia and radius of gyration for circular disc are to be determined.
Now, area of the disc, A = π r2
∴ Mass per unit area of the disc, ![]()
Now, let us consider a small circular strip of width dx at a distance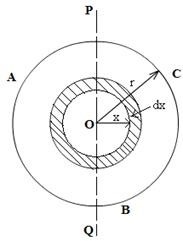
x from the center of the disc. (Fig right hand side)
The area of the strip,
dA= circomeference of the strip × width of the strip
=2πxdx
If dm is the mass of the strip, then
Now the moment of inertia of this strip about the axis PQ,
If we consider that the whole disc is composed of such like strips, then the moment for the whole disc can be obtained by integrating the above equation for the limits x = 0 to x = r.
So moment of inertia,
Let K be the radius of gyration,
Determination of Moment of inertia and radius of gyration of a rectangular lamina about an axis perpendicular to its center of mass:
Let, ABCD be a rectangular lamina of mass M and length, l = AB = CD and breadth, b = AD = BC (Fig right hand side). Let the axis of rotation XOY pass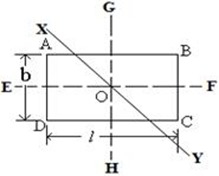
through the center and perpendicular to the lamina. Moment of inertia
and radius of gyration are to be determined.
Now, the axis EF passing through O is parallel to side AB and
axis GH passing through O is parallel to side AD. EF and GH are
perpendicular to each other. XOY axis is perpendicular to both EF
and GH.
According to perpendicular axis theorem, the moment of inertia of a lamina about the axis XOY,
Again, radius of gyration K is related to I as
MK2=I
Expression for centripetal acceleration and centripetal force:
Let us consider an object of mass m is moving along a circular path of radius r, in anticlockwise direction with a uniform speed v, and an angular velocity ![]() with at center O. When the body is come from A to B in small time variation t. The velocity at A is the Tangent along AC.
with at center O. When the body is come from A to B in small time variation t. The velocity at A is the Tangent along AC.
Now, in rectangular OAEB, we get
∠AEB+∠AOB =180°
Again, ∠AEB+∠BEC = 180°
The horizontal component of velocity at A, vy = 0
and the vertical component, vx = v
The vertical component of velocity along AC, vy = vsinθ
and the horizontal component, vx = vcosθ
when tis very small then θ is also very small
∴ sin θ = θ, and cos θ = 1
∴ the vertical component of velocity at B, vy = vθ
and the horizontal component, vx = v
It appears that, there is no change of velocity along horizontally,
So, centripetal acceleration,
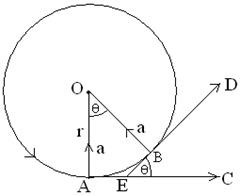
Motion of a cyclist along a curved path:
 A cyclist travelling along a curved path bends his body with the cycle
A cyclist travelling along a curved path bends his body with the cycle
Towards center of curvature. Without centripetal force the force acting
On the cyclist would have thrown him out of the road. To balance this
tendency of skidding the cyclist along with the cycle bends his body
towards the center. This is haw centripetal force is produced.
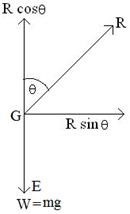
Let a cyclist moving at uniform speed von the circular path of radius
rbends away from the normal by an angle θ.
Let the weight of the cyclist along with the cycle be mg and the
Reaction force by the road on the cycle be R. R can be resolved in to two
rectangular component Rcosθ vertical to the ground and Rsinθ towards
the center of the circular path (Fig. Right hand side). The component Rcosθ
balances the weight mg and component Rsinθ provides the necessary centripetal force for the cyclist to move on the circular path. Now
So from above equation we conclude,
If the cyclist wands to turn the banking at higher speed speed he must bend more from the normal.
To download Laws of Rotational Motion (Part-2) in PDF format Click Here
To get Laws of Rotational Motion (Part-1) Click Here
Laws Of Rotational Motion (Part-2)
Laws Of Rotational Motion (Part-2)
Laws Of Rotational Motion (Part-2)
Laws Of Rotational Motion (Part-2)
Laws Of Rotational Motion (Part-2)