Laws of Rotational Motion (Part-1)

Laws of Rotational Motion (Part-1)

Laws of Rotational Motion (Part-1)

Introduction:

From Newton’s first law we know that everybody at rest or in linear motion tries to resist the change of stat because of inertia. Increase or decrease of inertia takes place with the corresponding increase or decrease of mass of body. Like linear motion there exist a type of inertia which resist the change of state of a body. This inertia depends on the masses of particles and their distribution with respect to rotation axis.

In case of rotational motion, like linear motion, there are velocity, acceleration, momentum, force etc. associated with the motion. So laws of motion associated with these terms are called laws of rotational motion. In this chapter we will discuss couple, moment of inertia, angular momentum, Newton’s laws of angular motion, torque, centripetal force etc.

Couple:

Definition: A pair of forces equal in magnitude, opposite in direction and not in the same line is called couple.

Explanation: Let, two equal forces are applied At point A and B of a rigid body [right hand side figure] these forces are parallel to each other and

oppositely directed. The line of action of forces is not along

the same line. Due to this couple the body will not be in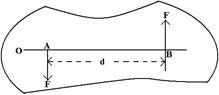

equilibrium; it will rotate. A body tends to rotate whenever

there is couple. When couple acts an a body, the

perpendicular distance between the forces is called arm of the couple. Moment of the couple is measured by the product of one of the forces and the perpendicular distance between the forces. If F a force of the couple and distance between them is d, then

momentum of the couple = F×AB = F×d

This moment can either be positive or negative. If the body rotates anti-clockwise due to the application of couple, then that moment is called positive moment and when it is clockwise, it is called negative moment.

Dimension of a couple:

Moment of a couple = Force × perpendicular distance

∴ Dimension =[MLT^-2×L] =[ML²T^-2]

Laws of Rotational Motion (Part-1)

Torque or Moment of a force:

A rigid body can rotate about a point. For example, a photograph can rotate about the point of contact between the nail and the thread from which the photograph is hanging; besides, the wheel of a vehicle can rotate about its axis.

The torque or moment of force about a chosen axis is the product of the force and its moment arm. It is denoted by (Tau).

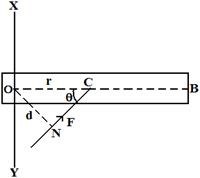Explanation: Let us consider a thin sheet AB fixed in horizontal

position in such a way that it can rotate about point 0 and

about the perpendicular axis XOY [Fig. 5’2]. If the sheet is

rotated by applying a force on any point, says C, it is observed

that,

1. Greater the magnitude of applied force greater is the

power to rotate.

2. Greater the distance between point O and the point of

application of force, the greater is the power to rotate.

3. If the line of action of the force is parallel to the plane of the sheet, it will not rotate Because of the above reasons; magnitude of the moment of force or torque is measured by the product of the magnitude of force and the perpendicular distance d of the action of force from the axis of rotation.

∴= d × F …. … … …. (1)

In above fig. ‘O’ distance of the point of action of the force = r, the line of action NC of the force = d and ∠NCO= θ.

So, ON = d = r sin θ

∴= d × F = rFsin θ

In vector form can be expressed as,

… … … … (2)

Here r and F are respectively position vector and applied force. The direction of is

perpendicular to the plane containing r and F. For anti-clockwise rotation, the direction of  is upward and its value is positive; whereas, for clockwise rotation, is downward and its value is negative.

According to equation (2), can be defined as:

Definition: For an object moving about an axis, the cross-product of the position vector of the point where the force is applied and the force is called torque.

Unit of torque or moment of a force: S. I. unit of t is Newton-meter (N-m).

Dimension: We know, = force × distance

= MLT^-2 × L = [ML² T^-2]

Moment of Inertia:

According to Newton’s law of motion, the force required to produce a given acceleration depends upon the mass of the body. Thus, the mass of a body is a measure of its inertia in linear motion.

A single force produces or changes the linear motion of a body. Similarly a couple causes or changes the rotatory motion of the body. The value of the couple required to cause a given angular acceleration does not depend only on the mass of the body. It also depends on the distribution of the mass about the axis of rotation. The inertia that a body possess for rotational motion is called its moment of inertia.

Definition: Moment of inertia is the sum of the product of the mass of each particle and the square of its distance from the axis of rotation.

Explanation: Let a rigid body of mass M rotating around an axis XY. Let the body be composed of particles of masses m₁, m₂, m₃………..placed at distances r₁, r₂,r₃ ……….
respectively from the axis.

The moment of inertia of the body about the axis of rotation is.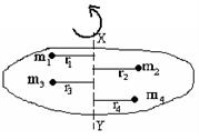

I = m₁r₁² + m₂r₂² + m₃r₃² + …………… +m_nr_n²

In the case of a body having a continuous and homogeneous distribution of matter,

Where dm is the mass of infinitesimally small element of the body at distance r from the axis.

Dimension of Moment of Inertia is ML² and unit is Kgm²

Radius of gyration:

We know, 

Let, the whole mass of the body be M.

If the whole mass of the body is concentrated at a distance K from the axis of rotation such that, I = MK², then K is called radius of gyration of the body about the axis of rotation.

Definition: The radius of gyration is the radial distance at which the mass of the body could be concentrated without altering the moment of inertia of the body about axis of rotation.

Equation of Kinetic energy of a rotating body:

Let a rigid body rotate about an axis at uniform angular velocity . Let the body is composed of particles of masses m_l, m₂, m₃………….placed at distances r₁, r₂, r₃………. respectively from the axis. Let their linear velocity are v₁, v₂, v₃……………………………………..

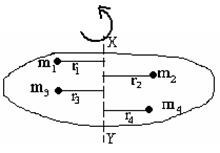So, Kinetic energy for the particle of mass m_l, k₁ = ½ m ₁v₁² = ½m₁ r₁²

Kinetic energy for the particle of mass m₂, k₂ = ½m₂v₂² =½ m₂r₂²

So, Kinetic energy of the body,

K.E.= k₁+k₂+k₃+……..+k_n

or, K.E.=½m₁ r₁² + ½ m₂r₂² + ½ m₃r₃² ……….+ ½ m_nr_n²

or, K.E.=½(m₁ r₁² + m₂r₂² + m₃r₃² ……….+ m_nr_n²)

or, K.E.=½I [∵I = m₁ r₁² + m₂r₂² + m₃r₃² ……….+ m_nr_n²]

When, unit, we get

K.E. = ½ I or, I = 2×(K.E.)

That is moment of inertia of a body rotating about a fixed axis at uniform velocity is numerically equal to twice the kinetic energy of the body. Alternately kinetic energy of a body rotating about a fixed axis at uniform velocity is numerically equal to half of its moment of inertia.

Laws of Rotational Motion (Part-1)

Relation between angular momentum and angular velocity ():

Let an object rotate about an axis with angular velocity. If the object is composed of many small particles, then we can write,

L = L_I + L₂ + L₃+ …….+L_n where, L₁, L₂, L₃,….etc. are the angular momentum of

individual particle.

Here L₁, L₂, L₃etc. are parallel to each other. Then,

L = r₁p₁+ r₂p₂ + r₃p₃ +……………..…+ r_np_n

or, L= r₁m₁v₁+ r₂m₂v₂ + r₃m₃v₃ +……+ r_nm_nv_n

This is the relation between angular momentum and angular velocity. From the above equation we can define angular momentum as follows.

The angular momentum of an object is the product of its moment of inertia about the axis of rotation and its angular velocity.

Relation with Torque and angular acceleration ():

 Newton’s Law for rotational motion:

There are three laws describing the relations between force, mass and motion,

when the body is in linear motion. These laws are known as Newton’s law of motion. Similarly, there are also three laws of rotational motion. These laws are discussed below.

First Law: In absence of external torque, a body in rest remains static, but the body in rotation rotates with constant angular velocity.

Explanation: In absence of any external torque on a body at rest continues in its state of rest and the rotating body rotates with uniform angular velocity.

Second Law: The rate of change of angular momentum of a body rotating about a fixed axis in it is directly proportional to the external torque applied and takes place in the direction of the torque.

Explanation: Let, a torque  applied on a body andis the change in angular momentum of the body. Then, according to this law,

Here K is proportionality constant. When,  unit and unit,

Then we get from above equation, k = 1

That is, the rate of change of angular momentum of a rotating body about a fixed axis is equal to the torque applied on it. This is another form of the second law.

We know, angular momentum, 

According to Newton’s second law of linear motion, F = ma

So,  , I and of rotational motion are analogues of F. m and a respectively of linear motion.

Third Law: To every external torque applied, there is an equal and opposite restoring torque. That is, the torque of action is equal and opposite to the torque of reaction.

Explanation: Let the torque applied by the body A on the body  and the torque applied by the body B on the body 

So, according to the law, 

 

To download Laws of Rotational Motion(Part-1) in PDF format Click Here

Laws of Rotational Motion (Part-1)

 

 Laws of Rotational Motion (Part-1)

Laws of Rotational Motion (Part-1)

Rotation around a fixed axis is a special case of rotational motion. The fixed axis hypothesis excludes the possibility of a moving axis, and cannot describe such phenomena as wobbling or precession. According to Euler’s rotation theorem, simultaneous rotation around more than one axis at the same time is impossible. If two rotations are forced at the same time, a new axis of rotation will appear.

 

This article assumes that the rotation is also stable, such that no torque is required to keep it going. The kinematics and dynamics of rotation around a fixed axis of a rigid body are mathematically much simpler than those for free rotation of a rigid body; they are entirely analogous to those of linear motion along a single fixed direction, which is not true for free rotation of a rigid body. The expressions for the kinetic energy of the object, and for the forces on the parts of the object, are also simpler for rotation around a fixed axis, than for general rotational motion. For these reasons, rotation around a fixed axis is typically taught in introductory physics courses after students have mastered linear motion; the full generality of rotational motion is not usually taught in introductory physics classes.