Laws of Motion Details With Diagram
Contents
Laws of Motion Details With Diagram

Laws of Motion Details With Diagram
Force:
“Force is that which changes or tends to change the rate of rest or uniform motion of a body along a straight line”. It is denoted by F. If the mass of a body is m, acceleration is a then force, F = ma. It is a vector quantity.
Fundamental Forces:
The force whose action-reaction are seen in the nature is called fundamental force. In other words, those force which are fundamental and do not originate from other forces, but all forces can be expressed in terms of those forces, are called fundamental force. All force in nature are classified in to four- classes; viz.
1. Gravitational force
2. Weak nuclear force
3. Electromagnetic force
4. Strong nuclear force
Description of the forces:
1. Gravitational force: In this universe, every particle of matters attracts every other particle with a force. This force is called Gravitational force. This force effects due to the particle graviton of the two bodies. They are interchanged to each other.
According to the law of gravitation, ![]() and
and 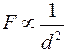 where m1and m2 are mass and d is the distance.
where m1and m2 are mass and d is the distance. 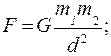 Where G = Gravitational constant.
Where G = Gravitational constant.
2. Weak nuclear force: The weak nuclear force is short–range force. It is effective inside the particle laptons. Due to this force, the radioactive β-decay is occurred. It has no range.
3. Electromagnetic force: This type of force is also called coulomb’s force. This force is developed due to the attraction –repulsion in static electric charges. This force is effective due to the exchange of photon (photon has no mass and charge). This force is stronger than the above two forces.
4. Strong nuclear force: The force is seen between the two nucleons in the nuclear. This force is the strongest among all other forces known. This force does not effective outside the nuclear of the atom. (Prof. Abdus salam and Weinberg tried and are trying to unify the forces.)
| Fundamental forces | Relative intensities | Range |
| 1. Gravitational force | 1 | Infinity |
| 2. Electromagnetic force | 1039 | Infinity |
| 3. Strong nuclear force | 1041 | 10-15 m |
| 4. Weak nuclear force | 1030 | 10-16 m |
Newton’s 1st Law of Motion:
“Everybody continue its state of rest or of uniform motion in a straight line if and only if it is not compelled by any external force to change that stat.”
Discussion of 1st law:
The 1stlaw of motion provides two concepts- (i) The inertia of a body (ii) the definition of force.
Inertia:
The inertia of a body is defined as that property of it, which tends to resist a change in its state of rest or of motion. More massive bodies have greater inertia. Hence mass is defined as quantitative measure of inertia.
Property of inertia may be of two kinds (i) inertia of rest and (ii) inertia of motion.
(i) Inertia of rest: The inertia of rest is the property of material bodies to persist in their state of rest. It is a common experience that a body remains at rest unless something is done to change the state. The body suddenly does not move out of its own accord.
Example of inertia of rest: When a motor car or any vehicle starts suddenly and rapidly gains
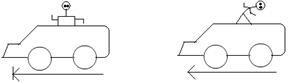
speed, a passenger standing or sitting unmindfully leans backwards. The lower part of his body being in contact with vehicle, shares its motion, but the upper part due to inertia of rest, tends to stay at rest. The man thus leans backwards.
(ii) Inertia of motion: The property of a body to continue in its uniform motion along a straight line is called its inertia of motion.
Example of inertia of motion: When a moving motor car or any vehicle suddenly stops, a passenger standing or sitting unmindfully falls forward. His lower part being in contact with the
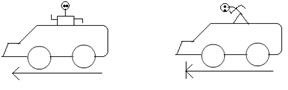
vehicle stops with it, but the upper part of the body continues moving forward so that the person learns forward.
Newton’s 2nd Law of Motion:
The rate of change of momentum of a body is proportional to the impressed force and it takes place in the direction of the straight – line in which the force acts.
Derivation of ![]() from 2nd law
from 2nd law
Let a body of mass m is moving with uniform velocity ![]() and the applied force on the body be
and the applied force on the body be![]() .
.
∴ Momentum of the body ![]()
So, the rate of change of momentum
![]()
According to Newton’s 2ndlaw of motion
![]()
![]()
![]()
![]()
![]()
Here K is proportionality constant we can show from the definition of unit force that K=1
Laws of Motion Details With Diagram
Definition of unit force:
The amount of force applied on a body of unit mass to create unit acceleration is called unit force.
![]()
Putting these values in equation (1) we get,
1.1=K.1
∴K=1
![]()
![]()
If forces ![]() act on a body then net force on the body is
act on a body then net force on the body is![]() .
.
So![]() in case of Newton’s second law can be written as,
in case of Newton’s second law can be written as,![]() the direction of
the direction of ![]() will be along the direction of net force
will be along the direction of net force ![]() acting on the body.
acting on the body.
1 Newton force: The newton is the SI unit of force; it is equal to the amount of net force required to accelerate a mass of one kilogram at a rate of one meter per second squared.
i.e. 1 Newton = 1kg ×1ms -2
Derivation of the 1st law from the 2nd law:
According to Newton’s second law of motion
![]()
When applied force, ![]()
![]()
![]()
![]()
∴ v =constant
When acceleration a = 0, then v =constant so there will not be any change in velocity. I.e. if no force is applied from outside, body at rest will remain at rest or the moving body will move will constant velocity. This is Newton’s first law.
Impulsive Force:
Impulsive force is a force of very high magnitude which acts for a short time.
Example: To hit a cricket ball by the bat, collision between trains, explosion of bomb etc.
Impulse of Force:
The product of the impulsive force and the time during which the force acts is called Impulse of force. It is denoted by J.
Explanation: Let a strong force ![]() act on a body for a very short time t. Then, the Impulse of force
act on a body for a very short time t. Then, the Impulse of force ![]()
If the force![]() acts on a body from time
acts on a body from time![]() to
to![]() and the time interval
and the time interval![]() is very small, then
is very small, then![]() can be express as
can be express as 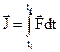
If![]() is constant then
is constant then 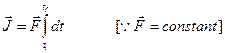
![]()
Relation with Impulse of Force and Momentum:
If the applied force is![]() then the Impulse of Force is,
then the Impulse of Force is,
![clip_image071[1] clip_image071[1]](https://saiftheboss7.files.wordpress.com/2012/10/clip_image0711_thumb.gif?resize=60%2C52&quality=100)
![]()
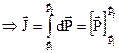
![]()
![]() So the impulse of force is equal to the change of momentum.
So the impulse of force is equal to the change of momentum.
 Newton’s 3rd Law of Motion:
Newton’s 3rd Law of Motion:
To every action there is an equal and opposite reaction.
Explanation: According to Newton’s third law of
motion forces always come in pairs, an action force
and its reaction force. If a body A exerts force, ![]() on another body B, then the body B will also exerts equal and opposite force on A. [Above figure]
on another body B, then the body B will also exerts equal and opposite force on A. [Above figure]
According to law, ![]()
Principle of Conservation of Momentum:
Principle: If no external forces act on a system of colliding objects, the total momentum of the objects in a given direction before collision = total momentum in the same direction after collision.
Following Newton’s law of motion the mathematical proof of the principal is given below:
Let two particles of mass m1 and m2 move in the same direction in straight line with velocity u1 and u2 respectively. Here u1 > u2. At one time the first particle hits the second particle from behind and then the two particles continue moving in the same direction and along the same line with velocities v1 and v2respectively.

Let the time of action and reaction due to collision be t, thus the resultant of initial momentum of the two particles ![]()
The resultant of the final momentum ![]()
According to the principal of conservative of momentum, it is to be proved that,
![]()
Proof: Rate of change of momentum of the first particle 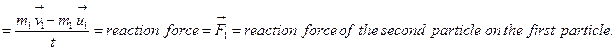
Rate of change of momentum of the second particle 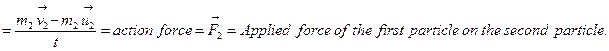
But, rate of change of momentum of the two particles (i.e. action force and reaction force) are equal and opposite, i.e.
![]()
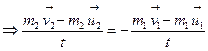
![]()
∴ Summation or resultant of the initial momentum of the two particles = summation or resultant of the final momentum of the particles.
![]()
So, no change of total momentum takes place due to the action and reaction force between two particles. In other words, the amount of momentum lost by the particle is exactly gained by the second particle i.e. momentum remain same before and after the collision.
Hence the conservation principle is proved.
Motion of Rocket:
The hot gases produced by the rapid burning of fuel ejected out at the backside of the rocket at a very high speed, the ejecting gas exerts a forward force on the rocket.
Explanation of Motion with the help of law of conservation of momentum.
If the air from a balloon is allowed to escape in the vertically downward direction, the balloon moves vertically upwards. A rocket is propelled in the forward direction in a similar manner. The rocket ejects gases in the backward direction. These gases produces from the combustion of the fuel in the rocket. Since the gases posses certain amount of momentum in the backward direction, the rocket has to move in the forward direction so as to conserve the total momentum.
Fuel:
Normally liquid hydrogen is used in rocket as fuel and liquid oxygen is used for combustion.
The equation of motion of rocket:
The ejecting gas exerts a forward force on the rocket which helps it in accelerating.
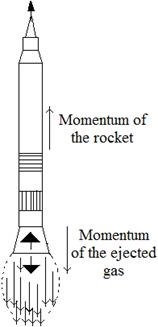 Let, the forward force = F
Let, the forward force = F
Mass of the rocket = M
In time interval dt, Mass of the ejected gas = dm
Velocity of the ejected gas with respect to rocket = v
∴ Change of momentum of gas in time interval dt = (dm) v
According to the law of conservation of momentum, change of
momentum of rocket in time interval dt, ∆P = (dm) v
∴ In absence of any external force (like gravity, air resistance)
Applied impulse on the rocket =Fdt = (dm) v
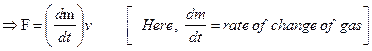
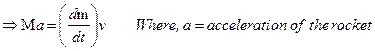
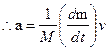
From the above equation, we conclude that,
(1) If injection velocity (v) of the gas is increased, acceleration of the rocket will increase.
(2) If the rate of injection of gas ![]() is increased, acceleration of the rocket will increase.
is increased, acceleration of the rocket will increase.
(3) If the total mass of the rocket (M) decreased, acceleration of the rocket will increase.
Equilibrium of Force:
Definition: If two or more forces act at a point or object and if the vector sum of all the forces acting on that point or object is zero i.e. ![]() , then that phenomenon is called Equilibrium of forces. Mathematically we can write,
, then that phenomenon is called Equilibrium of forces. Mathematically we can write, ![]()
 Lami’s Theorem:
Lami’s Theorem:
“If three non-parallel forces maintain equilibrium, then the magnitude of
any one is proportional to the sine of the angle between the other two.”
Let, three forces ![]() and
and![]() acting at a point O are in equilibrium.
acting at a point O are in equilibrium.
Angle between![]() , angle between
, angle between ![]() , angle between
, angle between
![]() , According to lami’s theorem,
, According to lami’s theorem, ![]()
Friction:
Definition: The force which opposes the motion of one body over another body in contact with it is called friction.
When we push a body with a small amount of force, it does not move. It means that some force is acting on the body acting in a direction opposite to the force of our push. A marble moving on the ground slows down or stops due to friction between the marble and the ground.
Thus friction always opposes the motion of the body.
Kind of friction:
Friction is of three types:
(1) Static Friction
(2) Kinetic Friction or Dynamic friction or Sliding friction
(3) Rolling Friction
Static Friction:
When an object does not slide along a surface on which it rests even through a force is exerted to make it slide, then the friction between the contact surfaces is called static friction.
Co-efficient of static friction:
When two bodies are in contact with each other, the ratio of limiting static friction and the normal reaction force is called the Co-efficient of static friction. It is denoted by µs. Let fs be the limiting static friction and R be the normal reaction force then the Co-efficient of static friction, ![]() . The unit of fs and R are same, so µshas no unit. It is a number.
. The unit of fs and R are same, so µshas no unit. It is a number.
Relation between angle of friction and angle of repose:
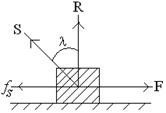 Angle of Static Friction:
Angle of Static Friction:
The resultant of the limiting static friction and the normal reaction forces
is called the “resultant reaction”. The angle between the resultant reaction
and normal reaction is called angle of friction. (Fig: right hand side)
Let, the normal reaction = R
Limiting static friction = fs
Resultant reaction = S
According to definition, the angles ⋋between S and R is angle of static friction.
From figure, ![]() and
and
![]()
From (2) and (3), ![]()
![]()
This is the relation between co-efficient of friction and angle of friction.
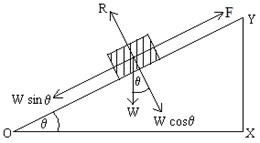
Angle of Repose:
The angle between the inclined plane and horizontal plane
for which a body tends to move is called angle of repose.
Explanation:
In right hand side figure a wooden block is kept on an
inclined plane OY-making an angle θ with the horizontal
plane. Let W be the weight F be the frictional force and R be the reaction force. Weight W of the body can be resolved in to two components.
The component along the normal to the inclined plane = W cos θ
The component along the inclined plane = W sin θ
W cos θ acts opposite to reaction force R and W sin θ acts opposite to F
Since the body is at rest,
∴W cos θ = R … … … (6) and W sin θ = F… … … (7)
Now, if θ increases, W sin θ also increases and F will increase.
Let, θs be the angle when the body tends to move i.e. when θ = θs, F=fs. So angle θs is angle of repose.
From, equation (7) we can write,
W sin θs = fs… … … (8)
In this condition,
W cos θs = R … … … (9)
Dividing equation (8) by (9), we get
![]()
Comparing equation (4) and (10), we get
tan ⋋= tan θs ∴ ⋋= θs
i.e. angle of repose = angle of friction.
Kinetic Friction:
The friction force present when one body moves slowly or slides over another body is known as kinetic friction Dynamic friction or Sliding friction.
Co-efficient of kinetic friction: The ratio of kinetic friction and normal friction is called Co-efficient of kinetic friction.
It is denoted by µk.
Let, kinetic friction = fk,
Normal friction = R,
Then, ![]() ,
,
The unit of fs and R are same, so µk has no unit. It is a number.
To Download Laws of Motion Details With Diagram in PDF format click Here
Laws of Motion Details With Diagram
Laws of Motion Details With Diagram
Laws of Motion Details With Diagram
Laws of Motion Details With Diagram
Laws of Motion Details With Diagram
Laws of Motion Details With Diagram
Laws of Motion Details With Diagram
