HSC Higher Mathematics 2nd Paper Note 6th Chapter Conics
HSC Higher Mathematics 2nd Paper Note 6th Chapter Conics. In mathematics, a conic section (or simply conic) is a curve obtained as the intersection of the surface of a cone with a plane. The three types of the conic section are the hyperbola, the parabola, and the ellipse. The circle is a special case of the ellipse and is of sufficient interest in its own right that it was sometimes called a fourth type of conic section. The conic sections have been studied by the ancient Greek mathematicians with this work culminating around 200 BC when Apollonius of Perga undertook a systematic study of their properties.
HSC Higher Mathematics 2nd Paper Note 6th Chapter Conics

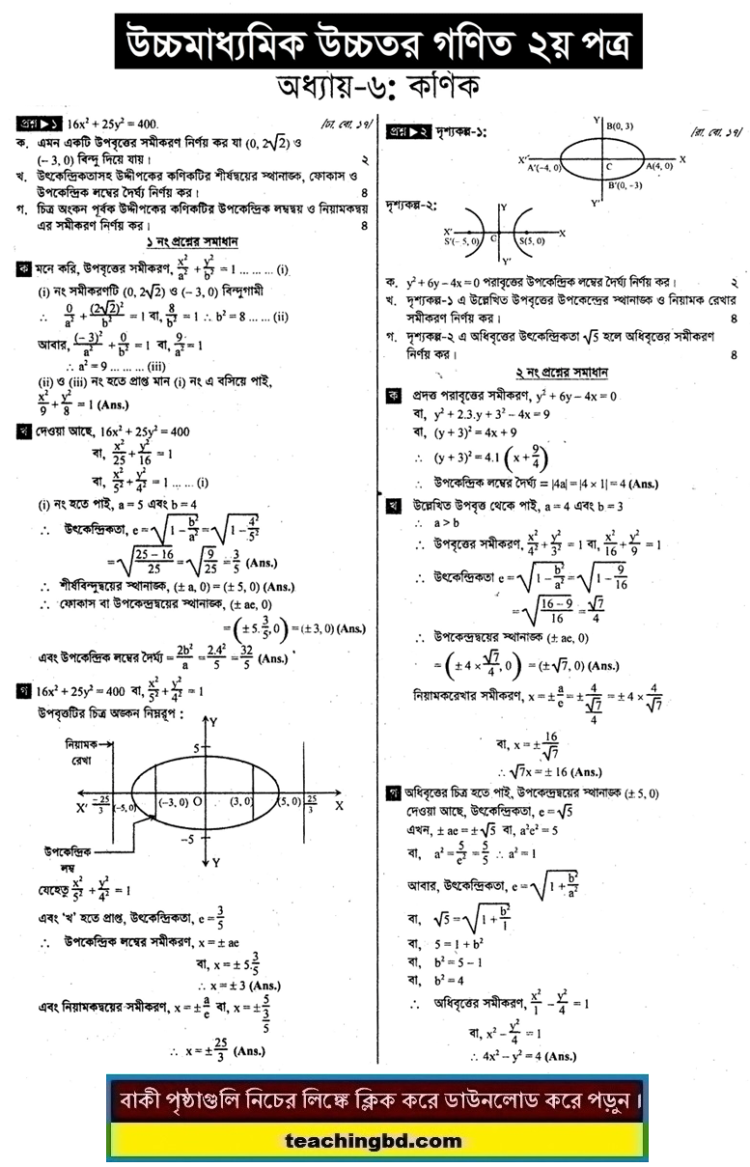
The conic sections of the Euclidean plane have various distinguishing properties. Many of these have been used as the basis for a definition of the conic sections. One such property defines a non-circular conic to be the set of those points whose distances to some particular point, called a focus, and some particular line, called a directrix, are in a fixed ratio, called the eccentricity. The type of conic is determined by the value of the eccentricity. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2; that is, as the set of points whose coordinates satisfy a quadratic equation in two variables. This equation may be written in matrix form, and some geometric properties can be studied as algebraic conditions.
teachingbd24.com is such a website where you would get all kinds of necessary information regarding educational noes, suggestions and questions’ patterns of school, college, and madrasahs. Particularly you will get here special notes of physics that will be immensely useful to both students and teachers. The builder of the website is Mr. Md. Shah Jamal Who has been serving for 30 years as an Asst. Professor of BAF Shaheen College Dhaka. He expects that this website will meet up all the needs of Bengali version learners /students. He has requested both concerned students and teachers to spread this website home and abroad.


