Two Dimensional Motion

Two Dimensional Motion

 

Two Dimensional Motion

Two Dimensional Motion

Questions: Deduce the equations below by vector method.

Let, a body moves with uniform acceleration, Let, at time t_i = 0, then initial position vector

, and initial velocity, Again time t_f = t, then final position vectorand final velocity

In physics, acceleration is the rate at which the velocity of a body changes with time.

When, t = 0, then and when t = t then, in this range, Integrate the above equation,

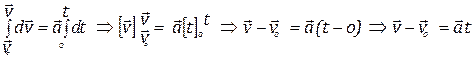
Let, a body moves with uniform acceleration, Let, at time t_i = 0, then initial position vector

, and initial velocity, Again time t_f = t, then final position vectorand final velocity

So, after t second the average velocity of the particle is

Let, a body moves with uniform acceleration, Let, at time t_i = 0, then initial position vector

, and initial velocity, Again time t_f = t, then final position vectorand final velocity

In physics, acceleration is the rate at which the velocity of a body changes with time.

When, t = 0, then and when t_f = t then, in this range, Integrate the above equation,

equation we get,

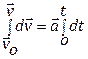
Since, the velocity of a moving body is defined as its rate of displacement so by the definition,

When, t_i = 0, then and when, t_f = t then, in this range, Integrate the above equation we get,

Let, a body moves with uniform acceleration . Let, at time t_i=0 then initial position vector and Initial velocity, Again time t_f = t then final position vector and final velocity.

In physics, acceleration is the rate at which the velocity of a body changes with time.

When, t= 0, then and when, t = t then, in this range, Integrate the above equation we get,

By dot product of we get,

Two Dimensional Motion

Projectile:

Projectile motion is the act of projecting an object into the air at an angle. A few real life examples of projectile motion are throwing a tennis ball, the motion of football, missile etc.

Two Dimensional Motion

Equation of motion of a projectile:

Let a projectile begin its flight from a point O (Fig: right side) Taking

O as Origin and let the horizontal and vertical direction be considered along

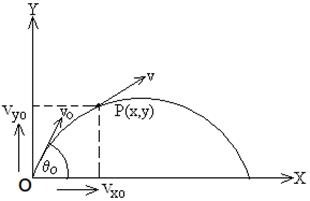X and Y-axis respectively.

Let the initial velocity or

velocity of projection = v_o

Angle of Projection = θ_o

The horizontal acceleration

of the projectile, a_x = 0;

The vertical acceleration of

the projectile, a_y = -g;

Since a_y is negative because

the direction of g is negative,

Since the point of projection

and origin is same, ∴ x_o = y_o = 0

The horizontal component of initial velocity = v_o cosθ_o

And the vertical component of initial velocity = v_o sinθ_o

The change of motion along X-axis is dependent on acceleration along X-axis.

The change of motion along Y-axis is dependent on acceleration along Y-axis.

At a certain interval of time t, the projectile cross the point P(x, y) where its velocity is = v

Then the acceleration along X-axis is, a_x = 0

Displacement along X-axis is = x

x = v_ocosθ_ot + ½a_xt²

or, x = v_ocosθ_ot + 0[∵a_x = 0]

or, x = v_ocosθ_ot

The acceleration along Y-axis is, a_y= g;

Displacement along Y-axis is = y

y = v_o sinθ_ot – ½gt²

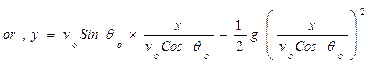[By putting the value of t]

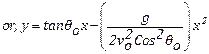
This is an equation of a parabola.  ∴  Path of motion of projectile is parabolic.

 

Questions: In case of Projectile Find the expression of (i) Required time to reach the maximum height (ii) Maximum height (iii) Time of flight (iv) Range (v) Maximum Range

(i) Required time to reach the maximum height:

Let a projectile begin its flight from a point O (In Fig) Taking O as Origin and let the horizontal and vertical direction be considered along X and Y-axis respectively. At a certain interval of time t, the projectile stay at the point P(x, y) where its velocity is = v

(i) Time to reach maximum height:

Vertical component of v_o isv_o sinθ_o

After time t, the final velocity at maximum height,

v_y = v_osinθ_o– gt………………(1)

But the velocity at maximum height, v_y= 0…………. (2)

By putting the value, v_y= 0, in equation (1)

(1) 0 = v_o sinθ_o – gt

(ii) Maximum height :

Let, the maximum height be H

∴H = v_o sin θ_o t – ½ gt²

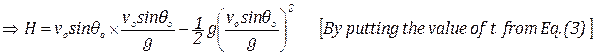
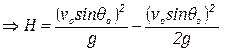
(iii) Time of Flight :

Let, the time of flight T i.e. is time taken from the point of projection and return to the ground is T.

Vertical displacement at time t, y = v_o sin θ _ot – ½gt². Let the time of flight be T. In time T the projectile returns to the ground. I.e. t = T and y = 0,

0 = v_osin θ _oT – ½gT²

or, ½ gT²= v_o sin θ_oT

(iv) Range :

Let, Range =R, R is the distance travelled along the horizontal direction in the time of flight T.

∴R = ( v_ocos θ _o ) × T

[By putting the value of T from Eq. (5)]

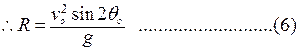
Maximum Range:

Let R_max be the maximum range, R will be maximum when sin2θ ₀ = 1

or, Sin2θ ₀ = Sin90⁰

or, 2θ ₀ = 90⁰

∴ θ₀ = 45⁰ so, if a body is thrown at an angle 45⁰ with the horizontal direction, the range will be maximum.

∴Maximum range,

Angular acceleration and proof of :

Angular acceleration of an object in circular motion is defined as the time rate of change of its angular velocity. it is generally denoted by α.

Letbe the change in angular velocity of the object in time interval t and while moving on a circular path, then angular acceleration of the object will be,

S.I unit of angular acceleration is rad s^-2.

We know that linear velocity v is denoted with angular velocity by by the relation

Differentiatingwith respect to time, we have

∴a=rα where a is the linear acceleration and α is the angular acceleration.

In terms of vector rotation, we have

 

Linear velocity and Angular velocity and Relation of :

 

Linear velocity:

The rate of change of displacement is called linear velocity. Velocity is the speed of an object and a specification of its direction of motion. Speed describes only how fast an object is moving, whereas linear velocity gives both how fast and in what direction the object is moving. The linear velocity of a moving body is defined as its rate of displacement. The linear velocity may be uniform or variable. It is donated by . It is a vector quantity and it’s unit is ms^-1. Velocity,

Angular velocity:

angular velocity of an object in circular motion is defined as the time rate of change of its angular displacement. It is denoted by.

Let, be the angle through which the body moves in time Angular Velocity; .

The unit of angular velocity is rad s^-1

The Dimension of angular velocity is

Relation:

Let us consider an object is moving along a circular path of radius r = OC=OB, in a anti clock wise direction with a uniform angular velocity. If the object rotted one turn in T second then angular displacement

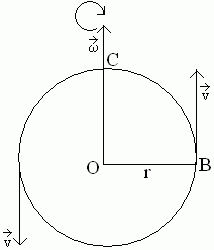Naw in T Sec. the object travels

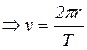
From equation (1) and (2) we gate

Linear velocity = angular velocity × radius of the circle.

Again, We know is a vector quantity and radius vector is also a vector quantity. Therefore, the cross product of two vectors will also be a vector. Let the resultant of the cross product

The magnitude of is

In addition, the direction are the same (according to the rule of cross-product)

So, from equation (4) and (5)

 

 

Difference between Angular Velocity and Linear Velocity:

 

Sl.no	Angular velocity	Linear velocity
1.	The rate of change of angular displacement is known as angular velocity.	The rate of change of linear displacement is known as angular velocity.
2.	It is denoted by	It is denoted by v
3.	Unit of it is rads-1	Unit of it is ms-1
4.	Dimensional equation of it is [T-1]	Dimensional equation of it is [LT-1]
5.	It does not depend on displacement.	It depends on displacement.

 

Centripetal Force:

The external force required to make a body moves along circular path with uniform speed is called centripetal force. Mathematically, the centripetal force required to move a body of massm along a circular path of radius r is given by,.

Centrifugal Force :

An object traveling in a circle behaves as if it is experiencing an outward force. This force, known as the centrifugal force, depends on the mass of the object, the speed of rotation, and the distance from the center. The more massive the object, the greater the force; the greater the speed of the object, the greater the force; and the greater the distance from the center, the greater the force. Mathematically, the centrifugal force required to move a body of mass m along a circular path of radius r is given by,.

Expression for centripetal acceleration and centripetal force:

Let us consider an object of mass m is moving along a circular path of radius r, in anticlockwise direction with a uniform speed v, and an angular velocity with at center O. When the body is come from A to B in small time variation t. The velocity at A is the Tangent along AC.

Now, in rectangular OAEB, we get

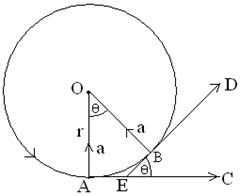∠AEB+∠AOB =180°

Again, ∠AEB+∠BEC = 180°

Spouse, ∠AOB = ∠BEC = θ

The horizontal component of velocity at A, v_y = 0

and the vertical component, v_x = v

The vertical component of velocity along AC, v_y = vsinθ

and the horizontal component, v_x = vcosθ

when t is very small then θ is also very small

∴ sin θ = θ, and cos θ = 1

∴ the vertical component of velocity at B, v_y = vθ

and the horizontal component, v_x = v

It appears that, there is no change of velocity along horizontally,

So, centripetal acceleration,

and Centripetal Force =

 To Download Two Dimensional Motion in PDF format Click Here

Two Dimensional Motion

Two Dimensional Motion

Two Dimensional Motion

Two Dimensional Motion

Two Dimensional Motion

Two Dimensional Motion