HSC EV Higher Mathematics 2nd Paper 2nd Chapter Note

HSC EV Higher Mathematics 2nd Paper 2nd Chapter Note. Linear Programming. Linear programming (LP, also called linear optimization) is a method to achieve the best outcome (such as maximum profit or lowest cost) in a mathematical model whose requirements are represented by linear relationships. Linear programming is a special case of mathematical programming (mathematical optimization). More formally, linear programming is a technique for the optimization of a linear objective function, subject to linear equality and linear inequality constraints. Its feasible region is a convex polytope, which is a set defined as the intersection of finitely many half spaces, each of which is defined by a linear inequality. Its objective function is a real-valued affine (linear) function defined on this polyhedron. A linear programming algorithm finds a point in the polyhedron where this function has the smallest (or largest) value if such a point exists.

HSC EV Higher Mathematics 2nd Paper 2nd Chapter Note. Linear Programming

Linear programming is the process of taking various linear inequalities relating to some situation and finding the “best” value obtainable under those conditions. A typical example would be taking the limitations of materials and labor and then determining the “best” production levels for maximal profits under those conditions. In “real life”, linear programming is part of a very important area of mathematics called “optimization techniques”. This field of study (or at least the applied results of it) are used every day in the organization and allocation of resources. These “real life” systems can have dozens or hundreds of variables or more. In algebra, though, you’ll only work with the simple (and graphable) two-variable linear case.

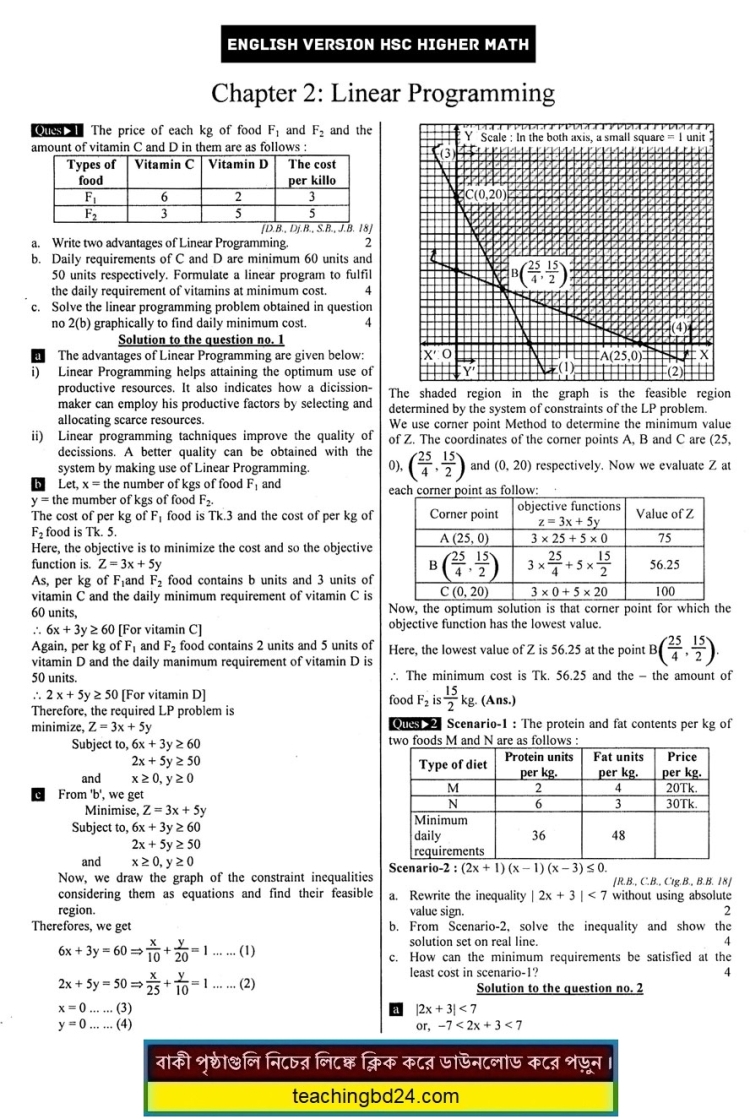
The general process for solving linear-programming exercises is to graph the inequalities (called the “constraints”) to form a walled-off area on the x,y-plane (called the “feasibility region”). Then you figure out the coordinates of the corners of this feasibility region (that is, you find the intersection points of the various pairs of lines), and test these corner points in the formula (called the “optimization equation”) for which you’re trying to find the highest or lowest value. Somebody really smart proved that, for linear systems like this, the maximum and minimum values of the optimization equation will always be on the corners of the feasibility region. So, to find the solution to this exercise, I only need to plug these three points into “z = 3x + 4y”

Determinants occur throughout mathematics. For example, a matrix is often used to represent the coefficients in a system of linear equations, and the determinant can be used to solve those equations, although more efficient techniques are actually used, some of which are determinant-revealing and consist of computationally effective ways of computing the determinant itself. The use of determinants in calculus includes the Jacobian determinant in the change of variables rule for integrals of functions of several variables. Determinants are also used to define the characteristic polynomial of a matrix, which is essential for eigenvalue problems in linear algebra. In analytic geometry, determinants express the signed n-dimensional volumes of n-dimensional paralleled.

Sometimes, determinants are used merely as a compact notation for expressions that would otherwise be unwieldy to write down. When the entries of the matrix are taken from a field (like the real or complex numbers), it can be proven that any matrix has a unique inverse if and only if its determinant is nonzero. Various other theorems can be proved as well, including that the determinant of a product of matrices is always equal to the product of determinants; and, the determinant of a Hermitian matrix is always real.

teachingbd24.com is such a website where you would get all kinds of necessary information regarding educational notes, suggestions and questions’ patterns of school, college, and madrasahs. Particularly you will get here special notes of physics that will be immensely useful to both students and teachers. The builder of the website is Mr. Md. Shah Jamal Who has been serving for 30 years as an Asst. Professor of BAF Shaheen College Dhaka. He expects that this website will meet up all the needs of Bengali version learners /students. He has requested both concerned students and teachers to spread this website home and abroad.

English Version HSC Higher Math Note